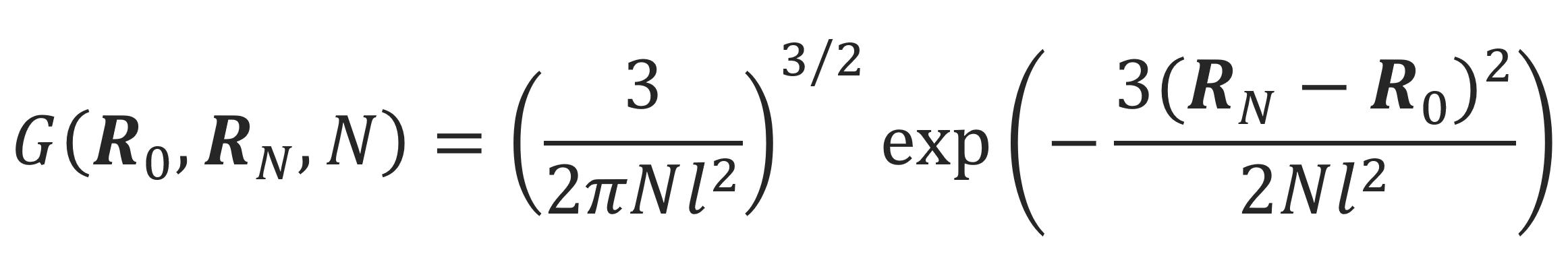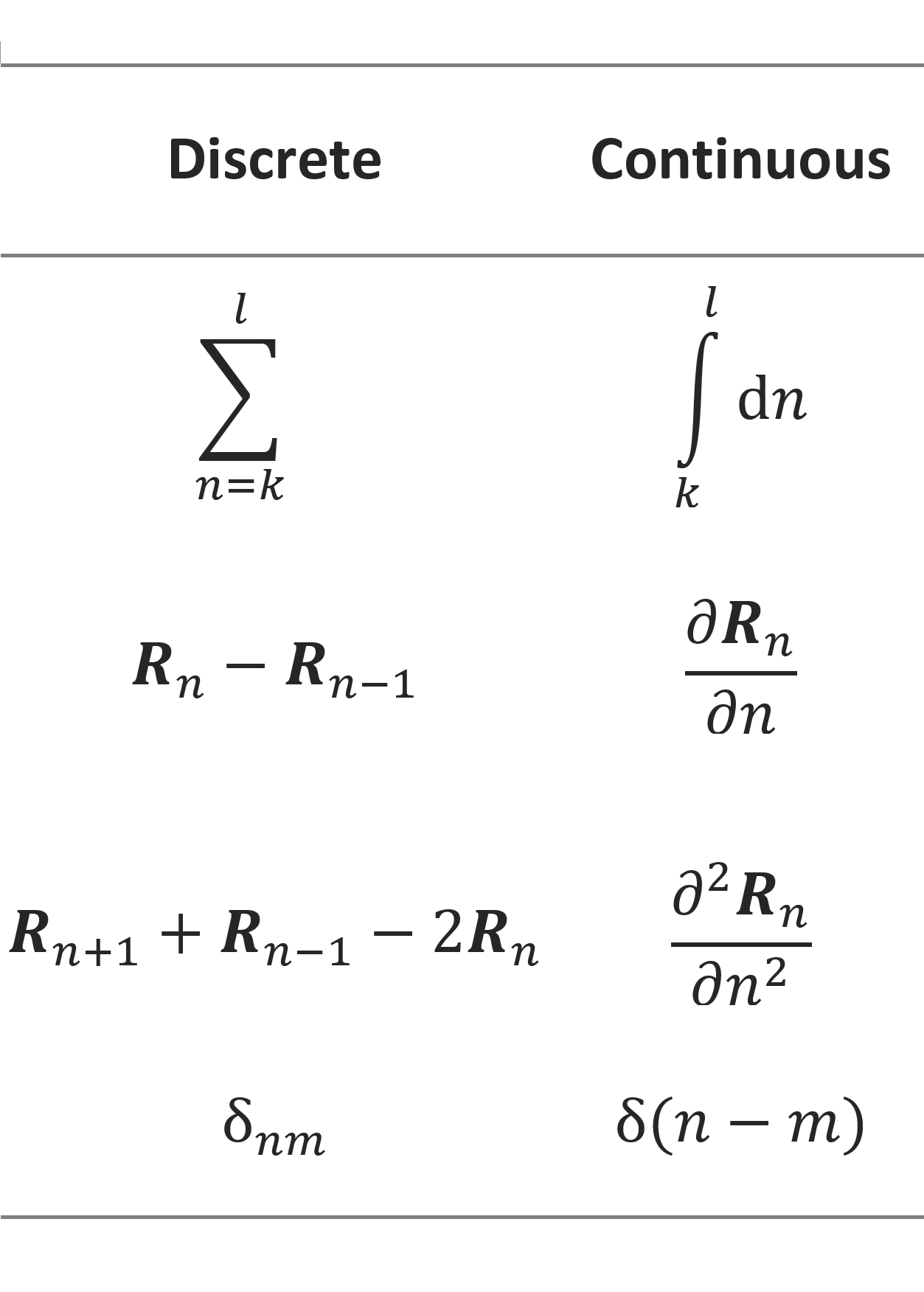Single Chain Mean Field Theory

The calculation of the local structure of a polymer chain and its related properties is extremely difficult and requires considerable computing time due to complex short-range and long-range interactions between monomers. Such attempts are often restricted to relatively short chains, i.e., to small degrees of polymerization, N. To simplify the calculations, scientist often choose coarse-grained models for polymer chains. These models can be subdivided into off-lattice and lattice models. Both types of models have their merits and lead to similar prediction for very long chains. In fact, as Doi and Edwards have shown, all discrete variables and operators of a lattice chain can be transformed to continuous ones.¹ Thus, equations derived for lattice chains can be easily converted to equivalent expressions for off-lattice chains.

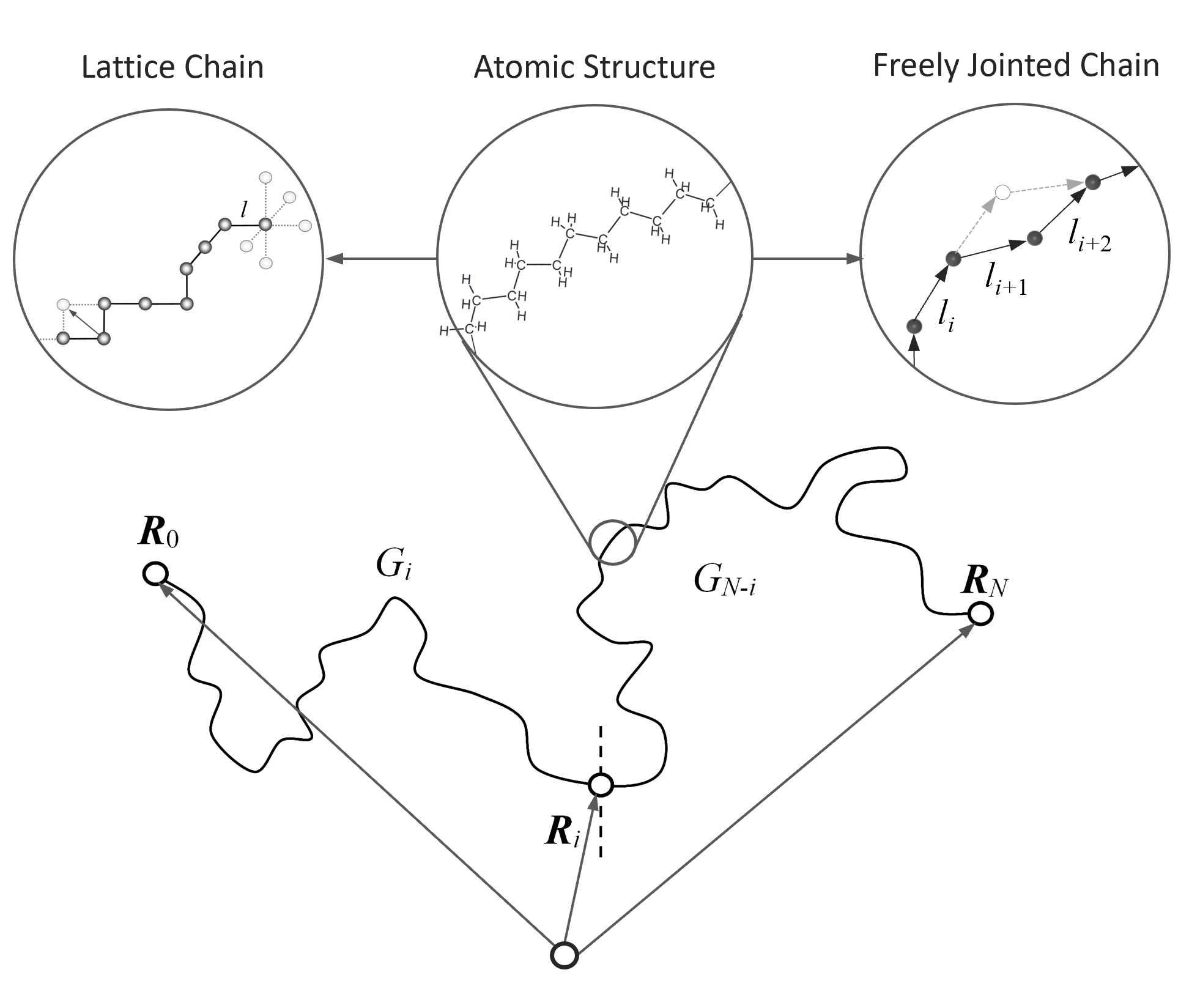
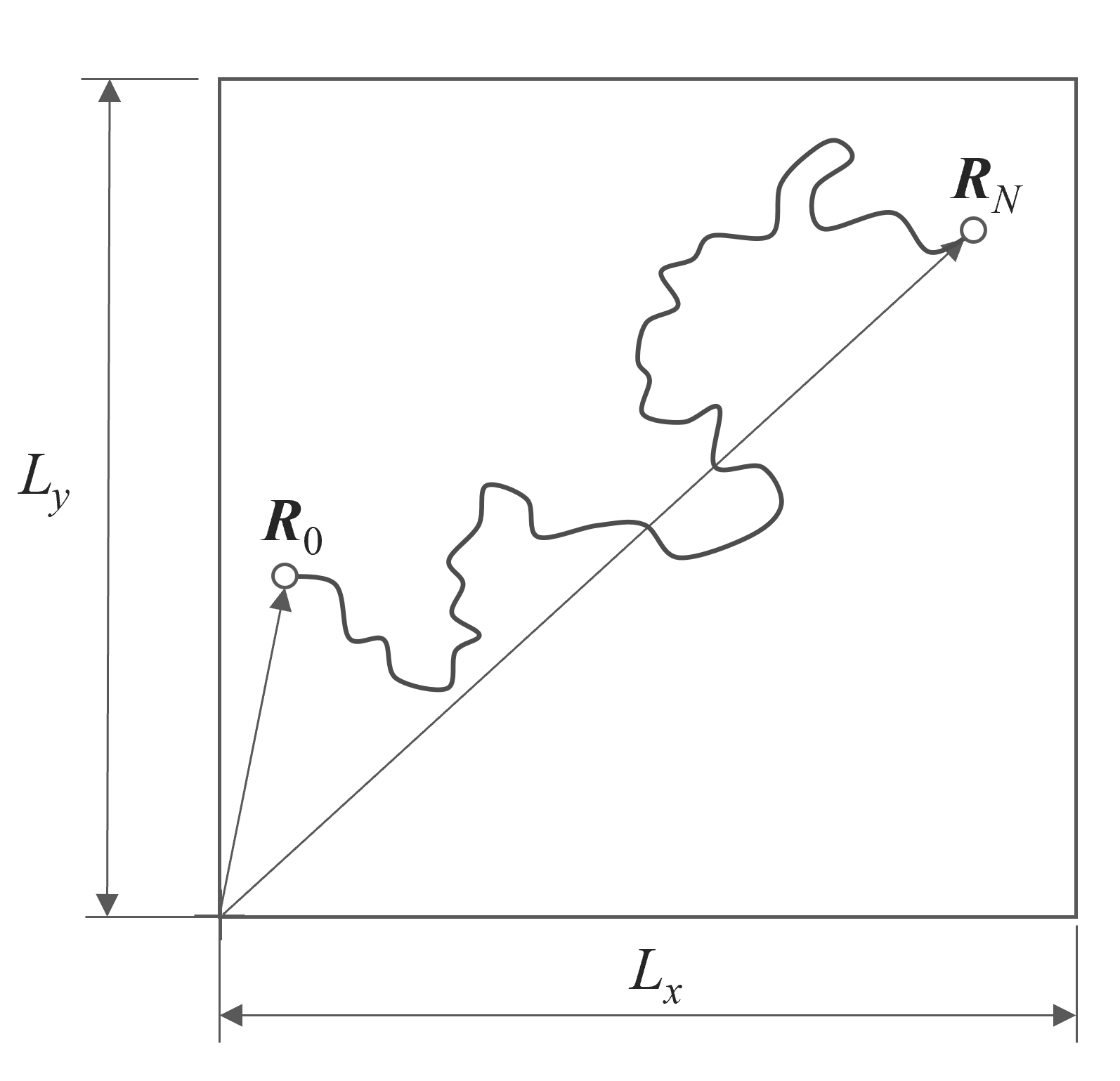
Let us consider first a chain with fixed bond lengths l. This chain can be constructed by attaching one bond after another consecutively. This model is equivalent to the diffusion of a free particle. Thus the polymer can be replaced by N bond vectors. If an external field is acting on the N segments, each conformation or bond arrangement has to be weighted by a Boltzmann factor:

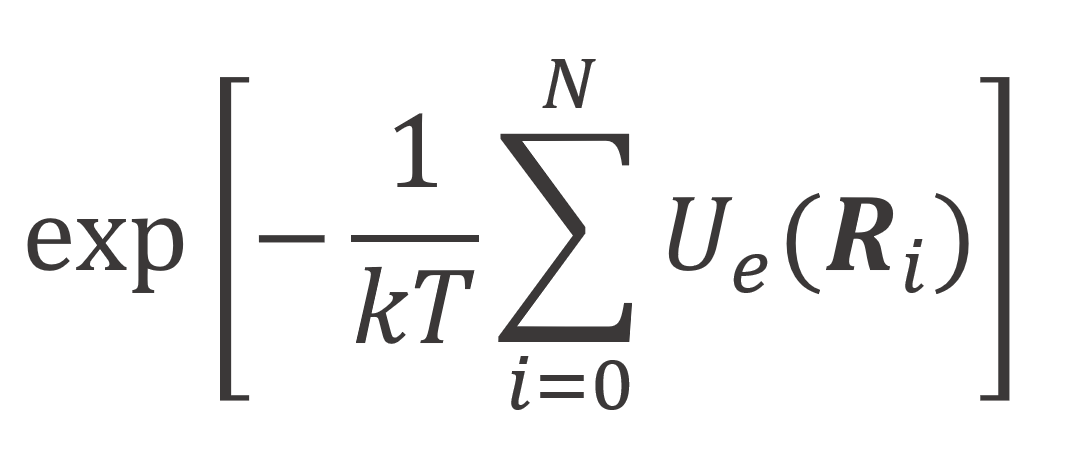
where U_e(R₀), U_e(R₁), ..., U_e(R_N) are the potentials at the spatial positions of the segments along the polymer chain.² The spatial distribution of the segments can be described with the segment distribution function G_N(R₀, R_N), the so-called Green function. This quantity is the probability that a chain starting at R₀ reaches the position R_N in N steps. This function can be calculated from a simple recursion relation: If the chain has reached the position R_N after N steps, then the position vector after N - 1 steps must be one of the adjacent sites, R_N - l_i . Each consecetive step has to be weighted with exp[-U_e(R_N)/kT] / z, where z is the number of adjacent sites that a segment can occupy. Thus, the probability of a chain being at R_N is given by⁹

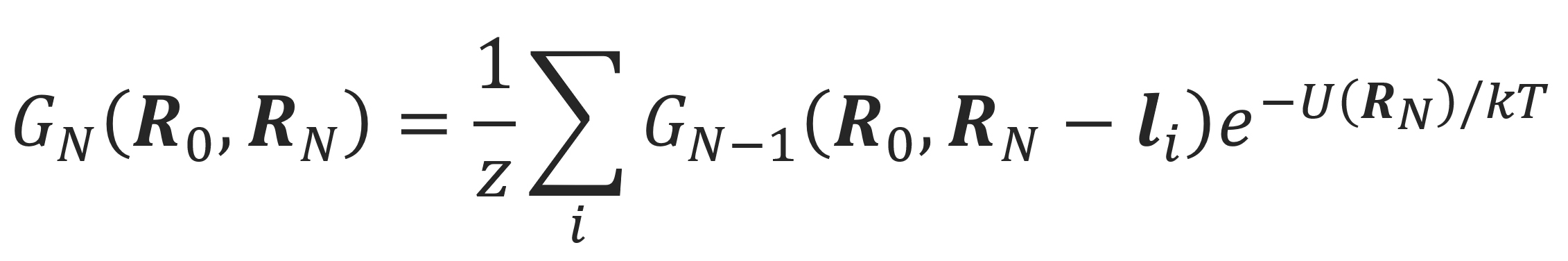
G_N(R₀, R_N,i) on the righ-hand side of the above equation can be expanded in terms of R as follows:³

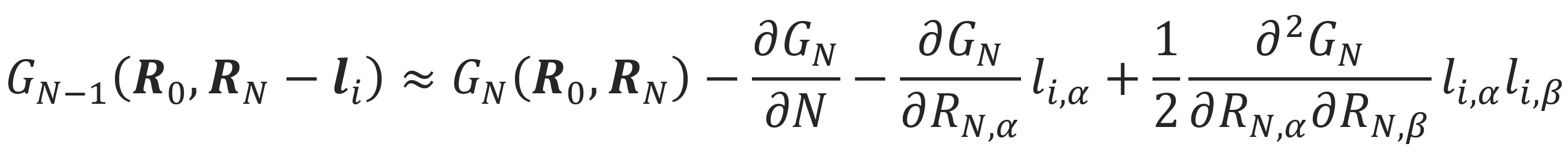
where R_N,α and l_i,α are the components of R_N and l_i following Einstein's convention for summation over repeated indices. Substitution of this series into the equation above and noting that:

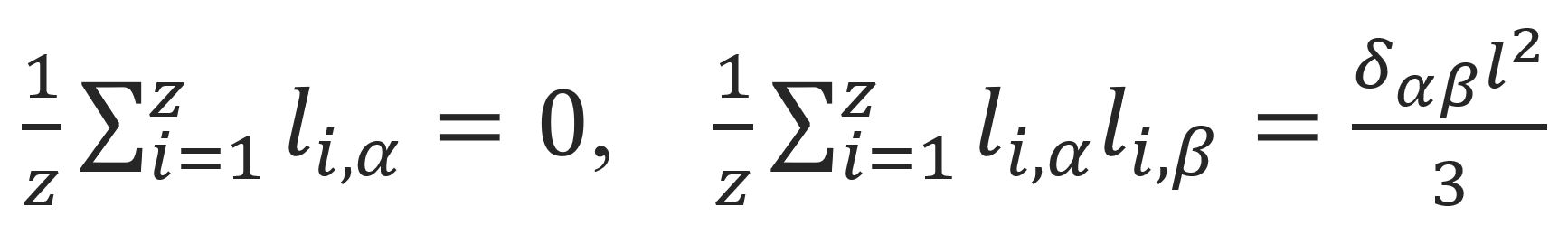
yields

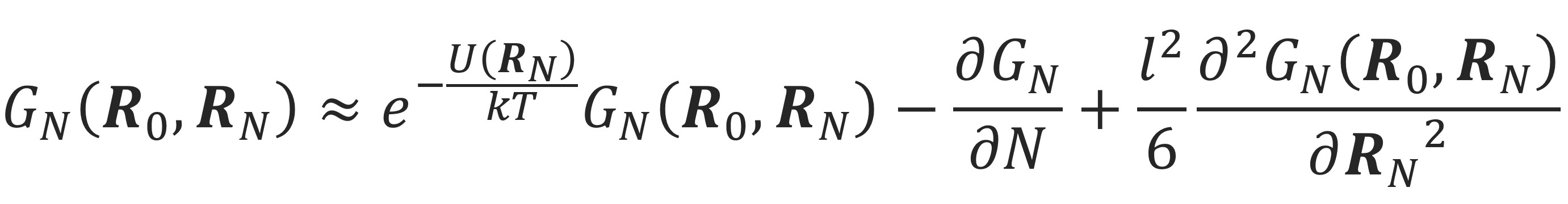
This differential equation may be simplified by expanding e^-U(R)/kT in a Taylor series up to the second order:

which yields⁴

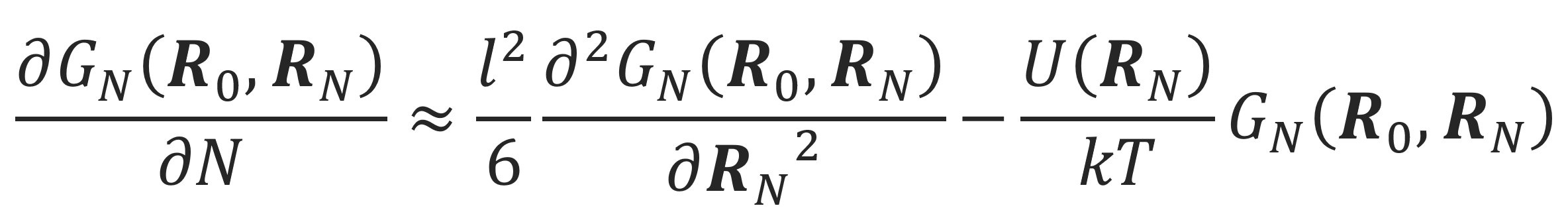
where U(R_N) is an as yet undetermined external potential. This equations is frequently called the Edwards equation,^5-7. It has the same form as the Schroedinger equation which has the general solution.^4,5

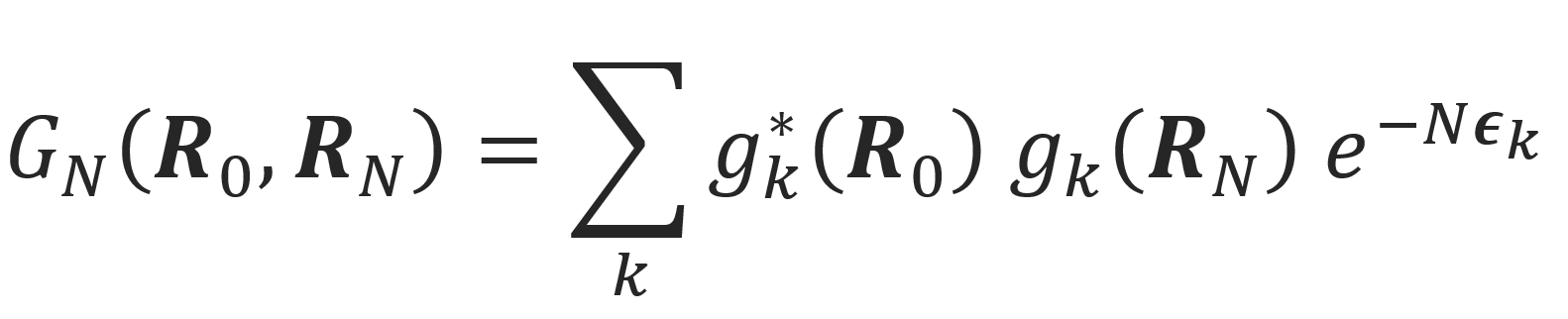
where g(k) are eigenfunctions and ε(k) are eigenvalues which are determined by:

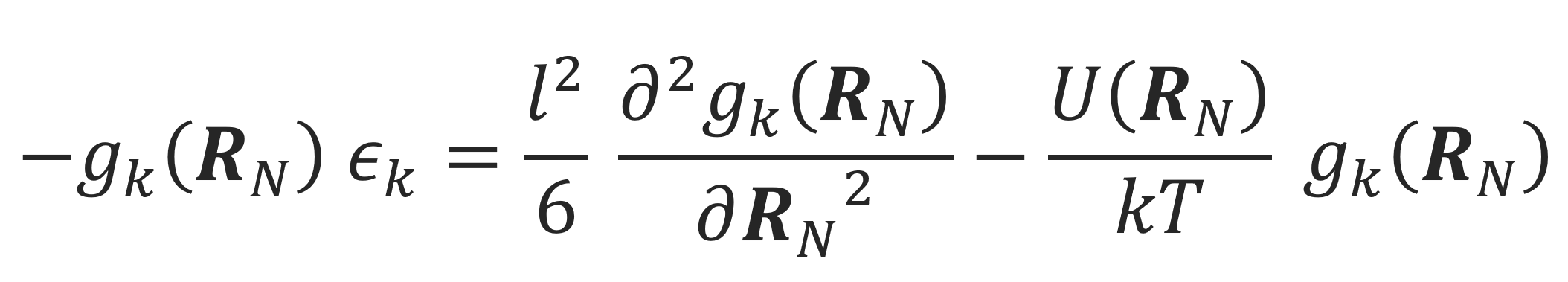
For very long chains, the ground state contribution in the eigenfunction expansion dominates and we may neglect all higher terms, which is the ground state dominance approximation:

Then the Edwards equation and segment density can be written as⁵

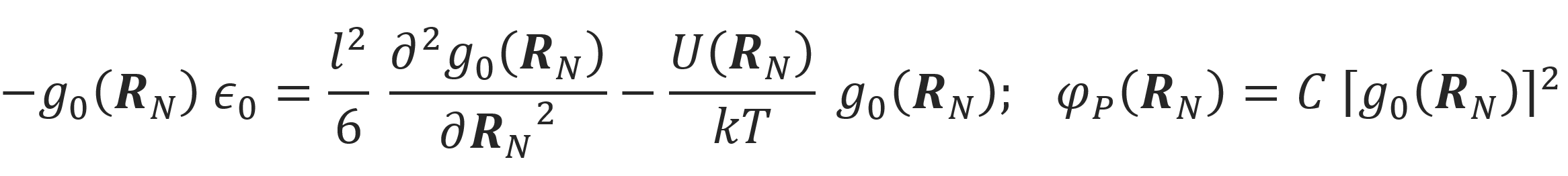
where C is normalization constant, which can be determined from the boundary conditions of the system in question.

Example:

As an example of the application of the Edwards equation, let us consider a linear ideal polymer chain confined in a box of volume V = L_x L_y L_z. In this case, the external potential is defined by the walls at which the potential is infinite whereas inside the box it is zero. The boundary conditions for this problem read

Since

the eigenvalues at the walls must be zero:

In the interval 0 < x < L_x, the external potential is zero, U(R) = 0. Then the Edwards equation reduces to

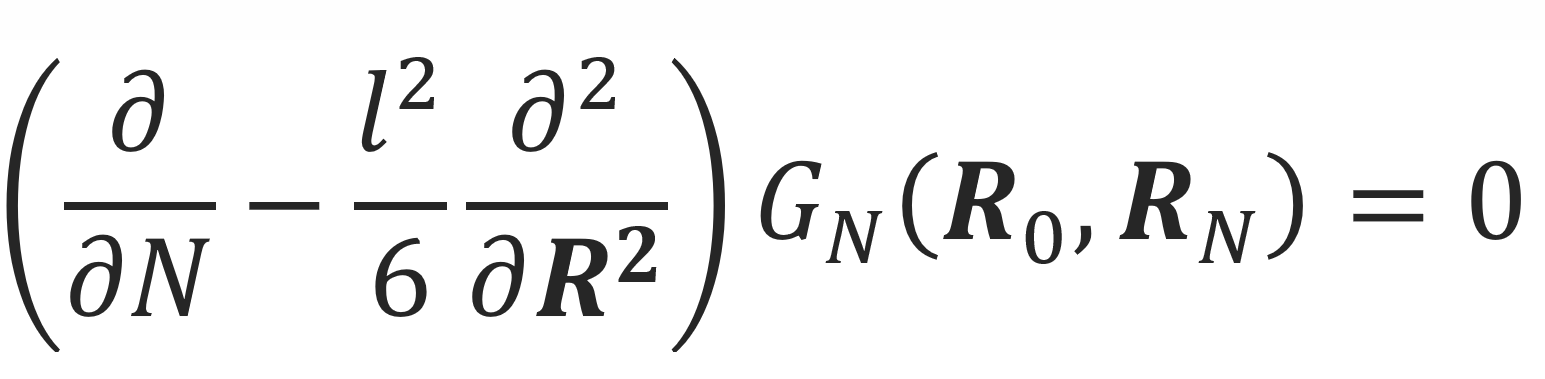
and

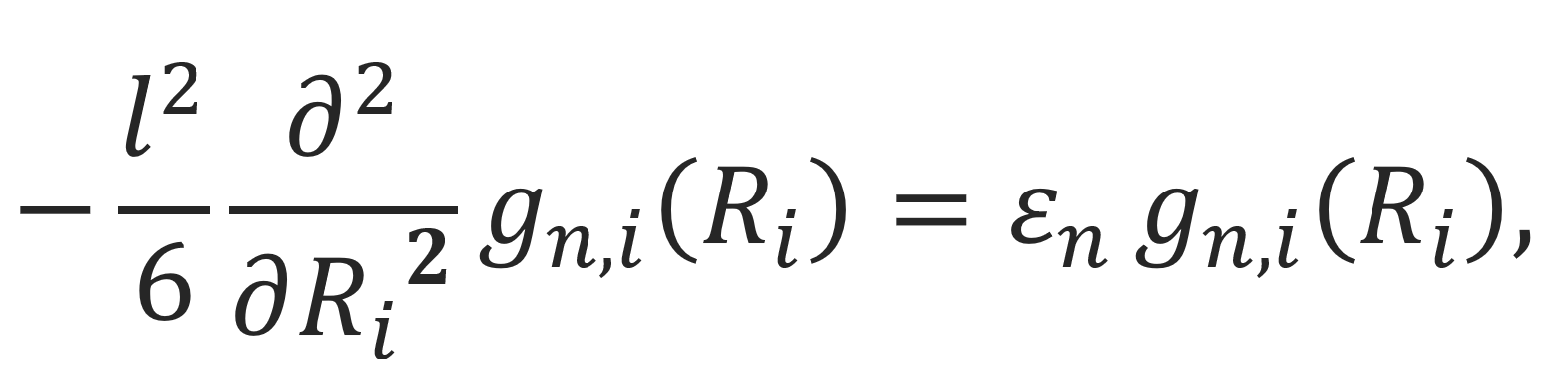
Under the above boundary conditions, these differential equations have following eigenfunctions and eigenvalues :

Then the general solution in each direction reads:¹

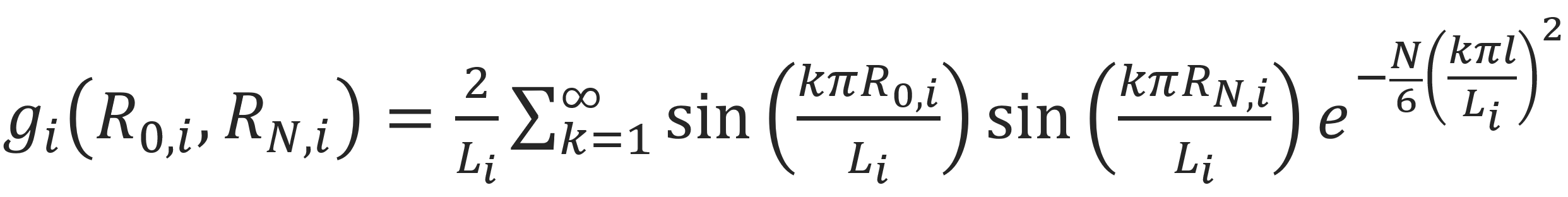
In the case N^1/2l >> L_x, L_y, L_z, i.e., if the relaxed chain is much larger than the box, the ground state dominates the series:

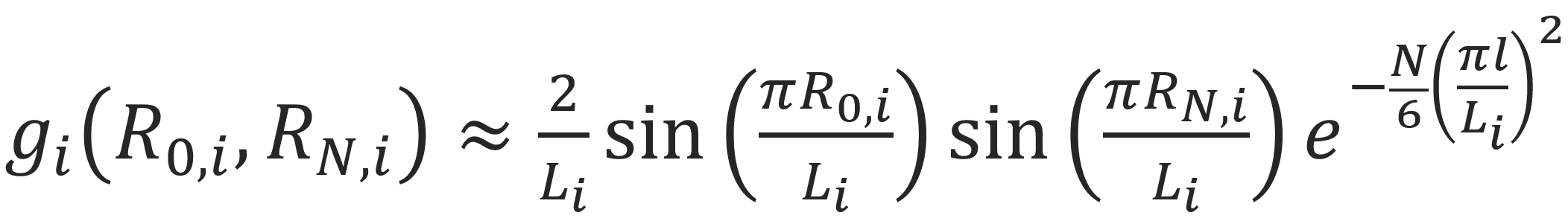
With this function we can readily calculate the properties of a polymer in a confined space such as the partition function, the radius of gyration, the pressure acting on the wall and the free energy of the system.¹

Edwards' mean-field method has been applied in many other problems. It is particularly useful when investigating polymers in inhomogeneous situations such as polymers near phase boundaries and adsorbed polymers.

References & Further Readings

1. M. Doi, S.F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, New York 1986

2. In the mean-field model of an excluded volume chain, the external potential is assumed being induced by the presence of other segments (excluded volume theory):^1,3

   

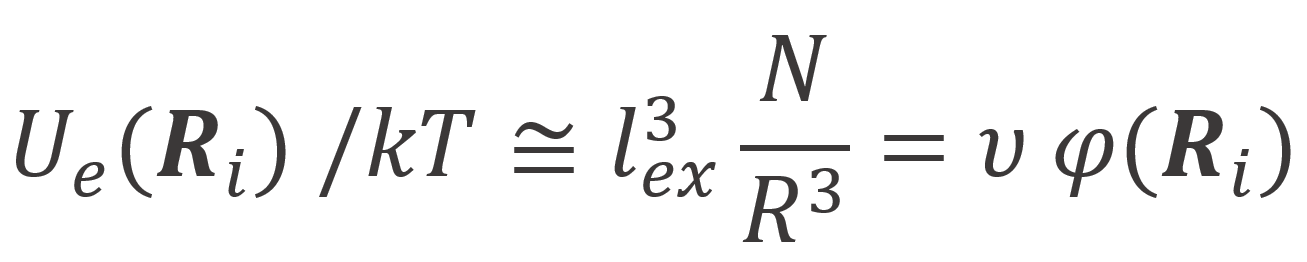
   where N/R³ is the average monomer density and υ is the effective volume of a segment. Note, υ can be negative which is the case when the attractive interaction between segments dominates, i.e. when monomers prefer other monomers to solvent molecules.

3. M. Doi, Introduction to Polymer Physics, Clarendon Press, Oxford 1995

4. S.F. Edwards, Proc. Phys. Soc. 85, 613 (1965) & 88, 265 (1966)

5. E.M. Blokhuis and K.I. Skau, J.B. Avalos, J. Chem. Phys. 119(6), 3483 (2003)

6. A. Johner, J. Bonet-Avalos, C.C. Linden, A.N. Semenov, J.F. Joanny, Macromol. 29, 3629 (1996)

7. K.I. Skau, E.M. Blokhuis, and J. van Male, Macromol. 37, 5, 1969 (2004)

8. G.J. Fleer, M.A.C. Stuart, J.M.H.M. Scheutjens, T. Cosgrove, B. Vincent; Polymers at Intefaces; Chapman & Hill, Cambridge 1993

9. In the absence of an external field, this function asymptotically approaches a Gaussian form for large N and negligible segment volume: